 Eiji Ogasa's website
Eiji Ogasa's website
 List of my papers
List of my papers
 Youtube 4次元・高次元・物理・数学・SFに
関係が有ります
Movies and Photos
Youtube 4次元・高次元・物理・数学・SFに
関係が有ります
Movies and Photos
 Twitter
Twitter
 Facebook
Facebook
 Instagram
Instagram
 ResearchGate
ResearchGate
 講談社website記事全部
講談社website記事各各
講談社website記事全部
講談社website記事各各
 Ogasa's English books
拙洋書
Ogasa's English books
拙洋書
 御仕事募集
御仕事募集
 日本SF作家クラブ
会員
日本SF作家クラブ
会員
 小笠英志
小笠英志
List of my books

Four-Dimensional Paper Constructions After Möbius, Klein and Boy
Series on Knots and Everything: Volume 78
タイトル↑をクリックすると出版社のwebsiteに行けます amazonでも購入できます Eiji Ogasaで検索して下さい
日本SF作家クラブのwebsite内の拙著の紹介欄です
 タイトル↓をクリックすると出版社のwebsiteに行けます amazonでも購入できます Eiji Ogasaで検索して下さい
タイトル↓をクリックすると出版社のwebsiteに行けます amazonでも購入できます Eiji Ogasaで検索して下さい
宇宙が見える数学
結び目と高次元―トポロジー入門
ブルーバックス・シリーズ
講談社
紀伊國屋1位(ブルーバックス・シリーズ 講談社)
紀伊國屋1位(トポロジー関連本)
紀伊國屋1位(トポロジー関連本)
紀伊國屋1位(結び目関連本)
紀伊國屋1位(講談社の数学の本)

4次元・高次元の一般向け入門書を英語で書いて海外の多国籍企業から商業出版しました
タイトル↓をクリックすると出版社のwebsiteに行けます amazonでも購入できます Eiji Ogasaで検索して下さい
Seeing Four-Dimensional Space and Beyond
Using Knots!
Eiji Ogasa
Series on Knots and Everything: Volume 74
日本SF作家クラブに掲載中の新拙著の紹介文
A movie to advertise my book
Seeing Four Dimensional Space and Beyond: Using Knots!
A movie related to my book
An instrumental secret of the Hopf link
A movie associated with my book
A scat from high dimensional space
アメリカamazon12位(differential geometry)
イタリアのアマゾンでチャートインしました(Bestseller in Matematica (in inglese))
アメリカのアマゾンでチャートインしました(Differential Geometry (Books))
日本のamazonで1位(algebraic geometry、洋書)

「多様体とは何か」ここをクリックすると試読(無料)のところへ行きます
講談社のブルーバックス・シリーズです
amazon1位
 紀伊國屋1位
紀伊國屋1位
 月刊誌「数学セミナー」日本評論社のランキングで1位
東大生協書籍部で新書全体の売り上げで2ヶ月連続Top10入り
月刊誌「数学セミナー」日本評論社のランキングで1位
東大生協書籍部で新書全体の売り上げで2ヶ月連続Top10入り
宇宙空間は無限か?有限か?
 有限としたら`はしっこ’はどうなってるの?
有限としたら`はしっこ’はどうなってるの?
 宇宙をまっすぐ進んで行くとどこに行くか?
宇宙をまっすぐ進んで行くとどこに行くか?
 宇宙全体の形はどうなってるの?
宇宙全体の形はどうなってるの?
 というSFクイズから始まります
(拙著 Part1)
というSFクイズから始まります
(拙著 Part1)
すべての数学・物理は多様体を
舞台に繰り広げられます
 数学・物理・SFの好きな方必携
数学・物理・SFの好きな方必携
多様体を基本から易しく解説
多様体の定義は皆さんならすぐ理解できるでしょう(拙著 Part1)
3次元多様体の例を作るあたりから
面白く(=手強く)なってきます。(拙著 Part1,2,3)
3次元多様体は`3次元’と名前についていますが、
3次元空間から飛びだして4次元空間・5次元空間に行ってしまうものもあります。
拙著では、4次元空間や5次元空間に描かれたその絵を披露します。(拙著 Part1,2,3)
そして、これらの多様体は案外日常生活で無意識に考えていることと同等なものだったりします。
なので多様体というのは自然かつ必要なものなのです
(拙著 §6 §14)
高次元多様体の話もします
未体験の興奮が味わえます
 ポアンカレ予想は解けてない?!
(拙著Part5)
ポアンカレ予想は解けてない?!
(拙著Part5)
 PDF版
PDF版
 という発展的な話題、未解決問題の紹介もします
という発展的な話題、未解決問題の紹介もします
拙著の序文と目次
10minutesTVのコラムで取り上げられました
dmenu ニュース (c) NTT DOCOMOさんで取り上げられました

「高次元空間を見る方法 次元が増えるとどんな不思議が起こるのか」
講談社のブルーバックス・シリーズです。
 amazon1位
amazon1位
第4刷が出ました
宣伝動画。
宣伝の静止画像。
講談社のウェブサイト内の拙著のウェブサイト
拙著の一部を試し読みできます
TBSラジオの番組アフター6ジャンクションで取り上げられました
日本評論社数学セミナーで取り上げられました

『相対性理論の式を導いてみよう、そして、人に話そう』 Click here.
(ベレ出版) 第二刷まで行きました。It went to second printing.
読者の皆様へ
本誌付随の動画、画像、
ここ
に有ります。
ここにも
有ります。
マイナス×マイナスがなぜプラスになるのかの小学生でも納得できる説明をこの本に書きました。 Click here.
オイラーの式
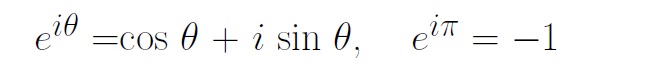 を高校数学で納得できる説明をこの本に書きました。
Click here.
を高校数学で納得できる説明をこの本に書きました。
Click here.
科学技術館のメルマガで取り上げられました クリックして2ページ目の赤印

『異次元への扉 ーーはさみと紙から始めてトポロジーの達人にーー』
Click here.
(日本評論社)
『読者の皆様へ
高次元を見て、高次元の図形を作る快感を、ぜひ皆様にも味わってもらいたいと願って書きました。
Click here.
『
異次元への扉 の最初の方に書いた問題です。
時間が有ったら考えてみて下さい。
うまく行くと、脳に異次元への扉が開いたような快感が味わえます。
Click here.
拙著に関連する動画と記事など
ボーイ・サーフェス設計図 です。是非工作してみて下さい。
ジュンク堂書店で取り上げられました クリックして2ページ目赤印

『4次元以上の空間が見える』
Click here.
(ベレ出版) 第三刷まで行きました。It went to third printing.
読者の皆様へ
Click here.
4次元以上の空間が見える の最初の方に書いた問題、2問です。
時間が有ったら考えてみて下さい。
1問目はSF小説やSF映画が好きなら小学生でも出来ると思います。
2問目は、やや難しいです。
Click here.
錐の体積=(1/3)×底面積×高さの公式の1/3はどうして1/3になる
のかの小学生でも納得できる説明をこの本に書きました。説明に使う簡単な図形の展開図を載せました。是非工作してみて下さい。
Click here.
正十二面体の対角線の長さを全て求める方法をこの本に書きました。正十二面体の工作についてコメントしました。よろしければ正十二面体を工作してみて下さい。
Click here.
帆船が風上の方へ進むことができることを感覚的に納得できる説明を書きました。手軽な実験で確かめられます。その実験も書きました
Click here.
日本評論社数学文化で取り上げられました
日本評論社数学セミナーで取り上げられました
週刊日本医事新報 日本医事新報社 2010年5月15日号No4490 P83 に拙記事が載りました。4次元空間についての短い初心者向け記事です
講談社のweb記事に
「マイナス×マイナス」は、なぜ「プラス」なのか?
--小学生にも納得できる説明とは!?--
という記事を書きました。是非御覧下さい。
yahoo newsにも載りました
講談社のweb記事に
『ブラックホールに吸い込まれると、どこに行くか? 宇宙の涯ての謎!
--宇宙好きは高次元や多様体が空想できる--』
という記事を書きました
拙著 多様体とは何か の紹介記事4本目でもあります。
是非御覧下さい 初心者向けです
yahoo newsにも載りました
講談社のweb記事に
『「ポアンカレ予想」はまだ解けていない!?』
という記事を書きました
拙著 多様体とは何か の紹介記事3本目でもあります。
是非御覧下さい 初心者向けです
yahoo newsにも載りました
講談社のweb記事に
『このクイズがとければ、4次元が見える!』
という記事を書きました
JAXA|宇宙航空研究開発機構のある相模原市のもと観光親善大使の方さんが、
4次元について皆様に問います。是非クリックして御覧になって御回答下さい。ヒント付です。
ヒントを検討したら必ず答に辿り着けます
講談社が書いた拙著の紹介記事1
講談社が書いた拙著の紹介記事2
講談社のウェブサイト内の拙著の内容の周辺についての記事
拙洋書宣伝動画
Seeing Four Dimensional Space and Beyond: Using Knots!
インストゥルメンタル・シークレット オブ ホップ・リンク
An instrumental secret of the Hopf link
高次元空間からのスキャットが聴こえますか
A scat from high dimensional space
マイナス×マイナスは なぜプラス?
を、天才姉妹(小学1年生と小学4年生)が
実質1分で説明してくれます。
小学生がわかる簡単な説明です。
クリックして是非御覧下さい。
元気が出ますよ
天才少女(小1)がポアンカレ予想について語ります。
是非御覧下さい
この方は
「解けばフィールズ賞間違い無し」の「有名未解決問題」
「4次元微分ポアンカレ予想」にアタック始めました。
その意気込みを語って下さいました。
応援してあげて下さい。皆さんもアタックして下さい。
JAXA|宇宙航空研究開発機構のある相模原市のもと観光親善大使の方さんが、
4次元について皆様に問います。是非クリックして御覧になって御回答下さい。ヒント付です。
ヒントを検討したら必ず答に辿り着けます
4次元・高次元空間に興味を持ち始めている皆様へ
トポロジー・チャイルド (Topology child 位相幾何の子) (小学4年生)から
重大告示があります
JAXA(宇宙航空研究開発機構)のある相模原市のもと観光親善大使の方さんが、
宇宙の涯てについて皆様に問います。是非クリックして御覧になって御回答下さい。ヒント付です。
ヒントを検討したら必ず答に辿り着けます
生まれて初めて高次元が見えた人が天地がひっくり返るほど驚いている瞬間を
動画に収めることに成功しました。皆さんも驚いて下さい。
拙著「高次元空間を見る方法」の関連動画。
`Make your Boy surface'
 ボーイ・サーフェスの紙工作
ボーイ・サーフェスの紙工作
 ボーイ・サーフェス設計図
ボーイ・サーフェス設計図
 A plan of Boy surface
A plan of Boy surface
Klein bottle can be made quickly
クラインの壺は簡単に工作できる
Klein bottle=2×Möbius band
クラインの壺=2×メビウスの帯
Klein bottle is made into (respectively, from) two Möbius bands.
This fact is understood easily by the craft in this movie.
「クラインの壺はメビウスの帯2個から作れる」「クラインの壺をメビウスの帯2個にわけられる」
ということが簡単に理解できる動画です。
拙著「高次元空間を見る方法」の宣伝の静止画像。
簡単な四次元の問題が載っています。よかったら考えてみて下さい
拙著「相対性理論の式を導いてみよう、そして、人に話そう」の宣伝静止画像2枚
My website in YouTube
*
New invariants for virtual knots via spanning surfaces
(with András Juhász, Louis H. Kauffman)
Journal of knot theory and its ramifications 2024
arXiv:2207.08129
[math.GT]
*
Quantum Invariants of Links and 3-Manifolds with Boundary defined via Virtual Links: Calculation of some examples
(with Heather A. Dye and Louis H. Kauffman)
arXiv:2203.12797
[math.GT]
*
Khovanov-Lipshitz-Sarkar homotopy type for links in thickened
surfaces
(with Louis H. Kauffman and Igor Nikonov)
arXiv2109.09245[math.GT]
A New Classical Link Invariant defined via Virtual Links and
Quantum Invariants of 3-Manifolds with Boundary
(with Louis H. Kauffman)
Journal of knot theory and its ramifications(2023)
https://doi.org/10.1142/S0218216523500426,
arxiv2108.13547[math.GT]
Khovanov-Lipshitz-Sarkar homotopy type for links in thickened higher genus surfaces
(with Louis H. Kauffman and Igor Mikhailovich Nikonov)
Journal of knot theory and its ramifications
(2021)
https://doi.org/10.1142/S0218216521500528,
arxiv2007.09241[math.GT]
*
Steenrod square for virtual links toward Khovanov-Lipshitz-Sarkar stable homotopy type for virtual links
(with Louis H. Kauffman)
arXiv:2001.07789
Local-move-identities for the Z[t,t^{-1}]-Alexander polynomials of 2-links, the alinking number, and high dimensional analogues
arXiv:1602.07775,
Journal of Knot Theory and its Ramifications Dallas Proceedings 2019.
(Conference on Knot Theory and Its Applications to Physics and Quantum Computing; 60th birthday of Jozef H. Przytycki, January 6-9, 2015
University of Texas at Dallas Richardson TX, USA)
Brieskorn submanifolds, Local moves on knots, and knot products
(with Louis H. Kauffman)
Journal of knot theory and its ramifications
(2019)
https://doi.org/10.1142/S0218216519500688
arXiv:1504.01229
A spinning construction for virtual 1-knots and 2-knots, and the fiberwise and welded equivalence of virtual 1-knots (with Louis H. Kauffman and Jonathan Schneider)
Photo of my coworkers and me:Click here.
arXiv.org > math > arXiv:1808.03023
Journal of Knot Theory and Its RamificationsVol. 30, No. 10, 2140003 (2021)
Special Issue: Proceedings of 6th Russian — Chinese Conference on Knot Theory and Related Topics (2nd Part)
The “unknotting number” associated with other local moves than the crossing-change
(Ribbon-move-unknotting-number-two 2-knots, pass-move-unknotting-number-two 1-knots, and high dimensional analogue)
Journal of knot theory and its ramifications (2018) https://doi.org/10.1142/S0218216518500517
arXiv:1612.03325
A new invariant associated with decompositions of manifolds
Journal of knot theory and its ramifications,
Volume 27 (2018)
//doi.org/10.1142/S0218216518500190
math.GT/0512320 (which includes hep-th/0401217)
Local moves on knots and products of knots (with Louis H. Kauffman)
Knots in Poland III-Part III Banach Center Publications Volume103
(2014), 159-209
Institute of Mathematics Warszawa 2014
arXiv:1210.4667[math.GT]
Local moves on knots and products of knots II
(with Louis H. Kauffman)
arXiv:1406.5573[math.GT],
Journal of Knot Theory and Its RamificationsVol. 30, No. 10, 2140006 (2021)No Access
Special Issue: Proceedings of 6th Russian — Chinese Conference on Knot Theory and Related Topics (2nd Part)
Local move identities for the Alexander polynomials of
high dimensional knots and inertia groups
Journal of knot theory and its ramificatioms vol18, no.4 (2009) 531-545,
math.GT/0512168, UTMS 97-63
Ribbon-moves of 2-knots: The Farber-Levine pairing
and
the Atiyah-Pathodi-Singer-Casson-Gordon-Ruberman
\widetilde\eta invariants of 2-knots
Journal of knot theory and its ramificatioms
Vol. 16, No. 5 (2007) 523-543
math.GT/0004007, UTMS 2000-22,
math.GT/0407164,
Supersymmetry, homology with twisted coefficients and n-dimensional knots
International Journal of Modern Physics A Vol. 21, Nos. 19 & 20 (10 August 2006), pp.4185-4196.
hep-th/0311136
Ribbon-moves of 2-links preserve the \mu-invariant
of 2-links
Journal of knot theory and its ramificatioms, vol13, no5 (2004) 669-687,
math.GT/0004008,
UTMS 97-35
The intersection of spheres in a sphere and
a new geometric meaning of the Arf invariant
Jornal of knot theory and its ramifications (2002), no. 8, 1211--1231 ,
University of Tokyo preprint UTMS 95-7,
math.GT/0003089 in http://arxiv.org/
Nonribbon 2-links all of whose components are trivial
knots and
some of whose band-sums are nonribbon knots
Journal of knot theory and its ramificatioms
10 (2001) 913-922, arXiv:1803.04581
The projections of n-knots which are not
the projection of any unknotted knot
Journal of knot theory and its ramificatioms 10 (2001)
121-132
,
math.GT/0003088, UTMS 97-34.
Singularities of projections of n-dimensional knots
Mathematical Proceedings of the Cambridge
Philosophical Society,
126 (1999) 511-519, UTMS96-39, arXiv:1803.03221
Link cobordism and the intersection of slice discs
Bulletin of the London Mathematical Society, 31 (1999) 1-8
arxiv 1803.02892
Some properties of ordinary sense slice 1-links:
Some answers to the problem (26) of Fox
Proceedings of the American Mathematical society
126 (1998) P.2175-2182, UTMS96-11, arXiv:1803.04586
The intersection of spheres in a sphere and
a new application of the Sato-Levine invariant
Proceedings of the American Mathematical society
126 (1998) PP.3109-3116, UTMS95-54,
arXiv:1803.03843
Intersectional pair of n-knots, local moves of
n-knots,
and their associated invariants of n-knots
Mathematical Research Letters (1998), 5, 577-582,
UTMS 95-50, arXiv:1803.03496
*
n-dimensional links, their components, and their
band-sums
math.GT/0011163, UTMS 2000-65, arXiv:math/0011163
*
A new obstruction for ribbon-moves of 2-knots:
2-knots fibred by the punctured 3-torus
and
2-knots bounded by the Poicar\'e sphere
arXiv:1003.2473[math.GT]
*
A new pair of non-cobordant surface-links which the Orr invariant, the Cochran sequence, the Sato-Levine invariant, and the alinking number cannot find
arXiv:1605.06874
My All papers are gotten from the following websites,
http://xxx.lanl.gov
http://www.ams.org
and those connected with them.
Almost all of my papers are also gotten from
the websites of the journals where my papers are published.
ResearchGate
 Seeing Four-Dimensional Space and Beyond
Using Knots!
Seeing Four-Dimensional Space and Beyond
Using Knots!
Eiji Ogasa
Series on Knots and Everything: Volume 74, World Scientific,
My book is cited in the website of
Science Fiction and Fantasy Writers of Japan,
a great organization of professional sci-fi writers etc.
A movie to advertise my book
Seeing Four Dimensional Space and Beyond: Using Knots!
A movie related to my book
An instrumental secret of the Hopf link
A movie associated with my book
A scat from high dimensional space
You can buy this book from the above website or Amazon.
My book charted in
Amazon USA Top12(differential geometry)
My book charted in
Italy Amazon
(Bestseller in Matematica (in inglese))and
America Amazon
(Differential Geometry (Books))
and
went to the top in
Japan Amazon
(algebraic geometry, written in languages other than Japanese)
List of Eiji Ogasa's Japanese books
(5)
What is manifold?
(This book is written in Japanese. Japanese title is
Tayotai to wa nani ka)
(4)
How to see high dimensional spcae
(This book is written in Japanese. Japanese title is
Kojigen kukan wo miru houhou)
(3)
Let's derive the identities of the theory of relativity, and talk about the way to your friends?
(This book is written in Japanese. Japanese title is
Sotaisei riron no
shiki wo michibiite miyou, soshite,
hito ni hanasou
)
(2) The door into different dimension
(This book is written in Japanese. Japanese title is
Ijigen e no tobira --hasami to kami kara hajimete topology no tatsujin ni
--)
(1) Seeing four dimensional space and beyond
(This book is written in Japanese. Japanese title is
4 jigen ijou no kuukan ga mieru)
List of Eiji Ogasa's introductory articles
(1)
Make your Boy surface
arXiv:1303.6448[math.GT]
Click
this for the movie of the paper-craft of making the Boy surface.
Japanese translation
(2)
Introduction to high dimensional knots
arXiv:1304.6053 [math.GT]
(3)
`An elementary introduction to Khovanov-Lipshits-Sarkar stable homotopy type'
(4)
Easy examples of explicit construction of
Khovanov-Lipshitz-Sarkar stable homotopy type
(5)
Seifert surfaces for virtual knots and Floer homology
Eiji Ogasa's profile
My interest is to see n-dimensional space and
to construct n-dimensional figures since my childhood.
I study topology and theoretical particle physics. My Phd thesis is on high dimensional knots and links. Now I am interested in `high dimensional knots and links' and its related topology.
I received Bachelor Degree (1992) from Math Dept., Univ
of Tokyo.
I received Master Degree (1994) from Math. Dept., Univ of
Tokyo.
I received PhD (1996) from Math.Dept., Univ. of Tokyo.
I was a DC fellow (1995-1996) and a
postdoctoralfellow(1996-2000)
of Research Fellowships of Japan Promotion of Science for
Young Scientists.
I was a postdoctoralfellow(2000), Faculty of Science, Univ
of Tokyo.
I was a COE postdoctoralfellow (2000-), Faculty of
Science, Univ of Tokyo.
I taught Einstein's theory of relativity at Kitazato University 2001-2006.
I taught math, physics, and computers atmany universities. Now I teach math at a University.
During 1997-2000 I lived in USA for two years.
I was a visiting researcher of Indiana University and that
of Brandeis University.
I had talks at Indiana Univ., Brandeis Univ., South
Florida Univ.
I stayed at Berkeley CA for three months, at Bloomington
IN for three months,
at Waltham MA for for one and a half year, Princeton NJ
for a half month, and Tampa FL for a half maonth.
While I stayed at the states, I went to congresses at UCBerkley, MSRI, Hravard Univ., MIT, IAS, Princeton Univ.
Photo:Click here.
Feb-March 2001 I visited Indiana Univ and had a talk.
2005 Feb March I stayed at Brandeis Univ.
I had a talk at Indiana Univ. and another talk at Brandeis Univ.
March, 2010, I attended String 2010 at Texas A&M university.
Sept 7, 2010, I talked at Topology seminor in Indiana Univ, Bloomington.
Sept 11, 2010, I talked at Knots in Chicago in Illinois Univ, Chicago.
Sept 14, 2010, I talked at Quantum Topology / Hopf Algebra Seminar in Illinois Univ, Chicago.
Sept 13, 15, 20, 2011, I talked at Quantum Topology / Hopf Algebra Seminar in Illinois Univ, Chicago.
Sept 9, 11, 16, 18, 2014, I talked at Quantum Topology / Hopf Algebra Seminar in Illinois Univ, Chicago.
Photo:Click here.
March 23, 27, 2018, I talked at Quantum Topology / Hopf Algebra Seminar in Illinois Univ, Chicago.
Photo:Click here.
April 1, 2020,
`A steenrod square for virtual links toward
Khovanov-Lipshitz-Sarkar stable homotopy type for virtual links'
based on my joint paper with Louis H. Kauffman
Skype seminar in Moscow and Beijing
organized by
Manturov.
People attended
from USA, England, France, Russia, China.
March 18,2021
`An elementary introduction to Khovanov-Lipshits-Sarkar stable homotopy type'
Quantum Topology / Hopf Algebra Seminar in Illinois Univ, Chicago, organized by Kauffman. On-line talk.
The file of the speech.
April 7, 2021,
`An elementary introduction to Khovanov-Lipshits-Sarkar stable homotopy type'
Skype seminar in Moscow and Beijing
organized by
Manturov. On line
The file of the speech.
April 8,2021
`Easy examples of explicit constrcution of Khovanov-Lipshits-Sarkar stable homotopy type'
Quantum Topology / Hopf Algebra Seminar in Illinoi Univ, Chicago, organized by Kauffman. On-line talk.
The file of the speech.
June 29, 2021
`Quantum invariants of 3-manifolds with boundary'
Seminars
on knot theory and related topics
organized by Manturov.
On line.
Sept. 22, 2021,
`Surgeries by 5-dimensional handles and 2-dimensional knots in the 4-sphere'
Skype seminar in Moscow and Beijing
organized by
Manturov.
On line.
November 9, 2021
`Quantum Invariants of Links and 3-Manifolds with Boundary defined via Virtual Links'
Fenn-Kauffman seminar On line
The file of the speech.
Dec 3, 2021
`Quantum Invariants of Links and 3-Manifolds with Boundary defined via Virtual Links'
Second Russia-Korea Conference on Knot theory and Related Topics. On line
April 13, 2022
`Quantum Invariants of Links and 3-Manifolds with Boundary defined via Virtual Links'
Moscow-Beijing Topology Seminar, organized by Prof. V.O. Manturov. On line.
Sept 17, 2022
Seifert surfaces for virtual knots and Floer homology
Geometry and topology of 3-manifolds
Sirius Mathematics Center, Sochi(Online)
November, 9, 2022,
Seifert surfaces for virtual knots and Floer homology
Moscow-Beijing Topology Seminar,
organized by
Manturov. On line
December, 21, 2022,
New Quantum invariants of classical links via virtual links
Moscow-Beijing Topology Seminar,
organized by
Manturov. On line.
August 9, 2023
Framed links in thickened surfaces and quantum invariants of 3-manifolds with boundary
Moscow-Beijing Topology Seminar,
organized by
Manturov. On line.
August 1, 2024
Seifert surfaces for virtual knots
Moscow-Beijing Topology Seminar,
organized by
Manturov. On line.
February 2, 2025,
Kauffman states
and
a new Khovanov-Lipshitz-Sarkar stable homotopy type
The International Knot Theory Congress,
Feb. 1-5, 2025 in honor of Lou Kauffman's 80th birthday, Online.
Are all 2-links slice?
April 2, 2025
Moscow-Beijing Topology Seminar,
organized by
Manturov. On line.
A Khovanov-Lipshitz-Sarkar homotopy type for links in thickened surfaces
Click this.
Click this, too.
Sept 18, 2025
Moscow-Beijing Topology Seminar,
organized by
Manturov. On line.
Photo of my coworkes and me, at Chicago, March 2018.

I visit Chicago Feb and March 2018.

I visit Chicago September 2014.

My hobby is windsurfin since 1995 summer.

I windsurf just for fun.

I started to play waterpolo 2005 spring. I had wanted to play it since my childhood.

I learned Aikido at MIT Aikido club a half year during 1999-2000.
I told the teachers there that I learned Judo in my childhood in Japan.
They are surprised.

E-mail adddress: pqr100pqr100(at)yahoo.co.jp
(please change (at) into @).
Last Updated, Aug 1, 2024.







 タイトル↓をクリックすると出版社のwebsiteに行けます amazonでも購入できます Eiji Ogasaで検索して下さい
タイトル↓をクリックすると出版社のwebsiteに行けます amazonでも購入できます Eiji Ogasaで検索して下さい




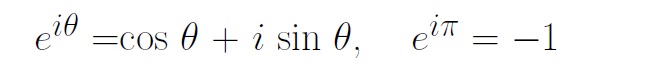 を高校数学で納得できる説明をこの本に書きました。
Click here.
を高校数学で納得できる説明をこの本に書きました。
Click here.
